【正文】

集合思想是数学的基本思想之一，它的内涵是把一类事物看成一个总体。自然，这一总体是以各个这样的事物为元素的。客观世界中任何两个事物总有差异，运用集合思想去看待它们，首先要善于把握研究角度，判断它们是否有某种共同性质，然后再把具有相同性质的事物看作元素，进而再把这些元素构成的整体看作“集合”。这是对事物的一种强有力的概括。集合、全集、子集、集合间的运算等，都反映了把事物或事物间的联系概括成总体或总体间关系的思想方法。集合思想的学习有助于帮助学生发掘问题的本质，把“零散”的单个问题归纳为共性问题，从整体的高度对问题进行全面、深刻的分析，进而提升学生的数学核心素养。

在初中阶段，集合思想的学习虽然不似化归、分类讨论、数形结合等数学思想那般常见和深入，但在不少地方都有其影子。作为教师，如何在教学中让学生感受集合思想、把握到集合思想的脉搏，对于学生数学学习的可持续发展有重要的意义。

一、概念分类教学中集合思想的渗透

在概念分类教学中，集合思想主要表现为两方面。一是将符合统一条件对象集中到一起；二是一个概念是另一个概念的一般化，或者说此概念是彼概念的特殊情形。

在教学活动中主要借助文氏图这一教学策略进行集合思想的渗透，引导学生初步感知集合思想，并运用集合思想解决一些数学问题。

例如：在沪教版数学六年级第一学期第1章“数的整除”中教学“素数”、“合数”等内容时，就会借助文氏图（如图1）的形式展开概念教学，帮助学生把握特殊与整体的关系，进一步理解抽象概念。

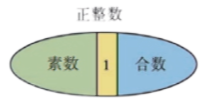
图1：正整数的分类

又如：在沪教版数学八年级第二学期第22章“四边形”中“特殊的四边形”之间的关系教学，通过让学生尝试补全文氏图（如图2）来进行教学，间接传达了子集思想、交集思想。学生不仅轻松地搞清楚了这些图形之间的内在联系，也在一定程度上提高了学生的抽象思维和概括能力，进一步完善了认知结构。

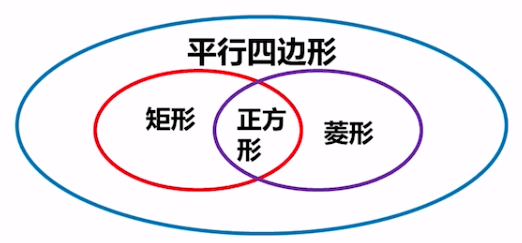
图2：平行四边形的分类

运用集合思想，借助“文氏图”的“形”还可以帮助解决实际问题，如：某班举办文艺晚会，演出歌舞节目的有12人，演出小品等节目的有 10人，两类节目都参加的有 4人，该班共有多少人参加这两类节目的演出？

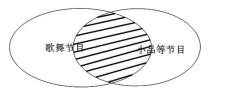
图3

将各种演出节目的人“数”转换为“形”，不仅更加突出了“分类”，还体现出了“公共（阴影）部分”（如图3）。学生借助文氏图进行直观分析，可知参加节目的总人数就是把所有图形代表的人数加起来的和。根据题意，只参加歌舞节目的人数是12-4=8（人），只参加小品等节目的人数是10-4=6（人）。所以三部分加起来就是8+6+4=18（人）。

文氏图犹如一座联结现实世界与数学概念的桥梁，是“用数学的眼光观察现实世界”的有效工具。在概念分类教学中借助文氏图进行集合思想的渗透有利于学生理解和辨析数学概念，有助于培养数学抽象这一核心素养。

二、方程与不等式教学中集合思想的渗透

在方程与不等式教学中，集合思想主要表现在借助数轴这一工具表示出满足方程或不等式（组）的数的集合。

在沪教版数学六年级第一学期第5章“有理数”中，随着数轴的引进，学生们体会到了最基本的“数形结合”，而此时表示有理数的点都可以在数轴上找到，但数轴上的点不一定表示有理数。学生带着这个认知，进入了沪教版七年级第二学期第12章“实数”的学习。随着有理数系向实数系的扩充，学生知道了任一实数都可用数轴上的点来表示；反之，数轴上的点也唯一对应了一个实数，即数轴上的点和实数是一一对应的。此时，教师可以向学生补充说明，数轴可以看作由无数个表示实数的点组成的集合，而这个集合里有相对“小”的集合，如整数集合、有理数集合、无理数集合等。

在沪教版数学六年级第二学期第6章“一次方程（组）和一次不等式（组）”的教学中，学生们首先知道了（非字母系数）一元一次方程的解有且只有一个，可以将其看成是一个单元素集合。在学习了一元一次不等式的解法后，学生们又知道了一元一次不等式的解集就是能让不等式成立的所有的解的集合，通常是一个范围。而一元一次不等式组的解集是要使所有不等式同时成立，即它们各自解集的公共部分（交集），当然也可能无解（空集）。

在教学时，初中教师常常会用到词语如“同时满足”、“有无公共部分”、“解集”等，而不会出现“交集”或者“空集”等数学术语。另外，在表示一元一次不等式组的解集时，初中学生也只是用一个不等式来表示，而这并不是集合描述法的正确表示格式。举一个简单的例子：求不等式组的解集。初中学生只要写出“1<x<2”即可，而高中学生则要写成或x∈（1，2）。因为根据初中数学学科基本要求，学生只需将一元一次不等式组的解集用不等式的形式表示出来，而无须用集合的形式表示。虽然初中没有出现与集合有关的专有名词和符号，但笔者认为可以借助数轴将其蕴含于一些直观的语言描述。例如将每个不等式的解集表示在数轴上后，可以说它们有无“公共部分”，不等式组的解集要“同时满足”每个不等式的解集，以此渗透“交集”、“空集”的概念。

借助“数轴”在方程与不等式的教学中进行集合思想的渗透，同时辅以“直观的语言描述”作为一种过渡，逐步培养学生“用数学的语言表达现实世界”，为高中阶段深入学习“集合与逻辑”打下基础。

三、函数图像教学中集合思想的渗透

在函数图像教学中，集合思想主要表现为满足函数解析式的点坐标与此函数的图像上点的一一对应关系。

在沪教版数学七年级第二学期第15章“平面直角坐标系”中，平面直角坐标系的建立把学生带入了二维空间。学生们知道了平面直角坐标系内的任意一点都可以用有序实数对来表示；反之，有序实数对也可以在平面直角坐标系中找到唯一一点。教师可以向学生补充说明，平面仍然看作是点的集合，但它与数轴上的点相比多了一个方向的属性，是一个二维的点。所以每个点和一个有序实数对 （x，y）是一一对应的。在此种观念下，两条坐标轴分别变成了具有共同特征属性的点的集合，即x轴上点坐标的纵坐标都是0，x轴便可以表示为直线y=0；同样地，y轴可以表示为直线x=0。函数关系式体现的就是那些符合表达式的有序实数对的共同特征，而这些有序实数对所对应的点的集合就构成了函数的图像。在沪教版数学八年级第一学期第18章“正比例函数和反比例函数”中，学生第一次接触到了函数图像的画法，即通过列表、描点、连线三个步骤来绘制正比例函数的图像。但在实际的操作过程中，学生不可能把所有满足函数解析式的点都列出来绘制出完整的函数图像。在初中阶段，教师只能这样告诉学生：“满足函数解析式的点都在函数图像上，在函数图像上的点的坐标都满足函数解析式。”以此辅助说明正比例函数的图像是一条直线。在函数图像的教学过程中，集合思想的渗透是通过先描出符合函数解析式的点坐标，再将这些拥有共同属性的点“集合”在一起，形成函数图像。让学生感受到函数图像是一个满足函数解析式的点集，从而在平面直角坐标系内形象地得到函数图像。借助集合思想的渗透来帮助学生进一步理解函数图像。

用好“满足函数解析式的点坐标与此函数的图像上点的一一对应关系”这一集合思想也是解决函数综合问题的重要且有效方法。例如：（2020年上海中考第24题第2小题）如图4，在平面直角坐标系xOy中，直线y=−x+5与x轴、y轴分别交于点A、B，抛物线y=ax²+bx（a≠0)经过点A. 如果抛物线y=ax²+bx经过线段AB上另一个点C，且BC=，求抛物线的表达式。

根据题意，要求抛物线的表达式，则
需要先求出点C的坐标。可以这样帮助学生
分析：由于点C在线段AB上，将线段AB
看成一次函数图像的一部分，那么根据“满足函数解析式的点都在函数图像上，在函数图像上的点的坐标都满足函数解析式”的一一对应思想，满足解析式
y=−x+5的点都在线段AB上的点，在线段AB上的点的坐标都满足解析式
y=−x+5。因此可设C（m，−m+5）。再根据BC=，利用两点间的距离公式即可求出点C坐标。

借助满足函数解析式的点坐标与此函数的图像上点的一一对应关系，在函数图像教学中进行集合思想的渗透，有助于学生在解决数学问题时以数解形或以形助数，感悟“数”与“形”之间的联系。

四、几何轨迹教学中集合思想的渗透

在几何轨迹教学中，集合思想主要表现为平面上的点经过运动形成新的几何图形，即常说的“点动成线”。平面几何图形都可以看成由无数独立而又连续的“点”所构成，所以可以用笔尖这个“点”画出一些几何图形，比如射线、直线、圆等。

在沪教版数学八年级第二学期第19章“几何证明”中，进行“轨迹”的教学时，如果从集合的观点出发，可以让结论更具有一般性。例如，可以先让学生们思考并进行操作：尽可能多地画出“到线段两端点距离相等的点”。然后提出问题：这些点集合在一起构成了什么图形呢？最后，在此基础上进行多媒体演示。从而让学生直观的感受到“线段的垂直平分线上任意一点到这条线段两个端点的距离相等”，而反过来“把到线段两端点距离相等的所有点集合在一起”构成了线段的垂直平分线。即到线段两端点距离相等的点的集合是线段的垂直平分线。

线段的垂直平分线、角的平分线、圆是初中阶段的三种重要“轨迹”。与上述垂直平分线教学类似，教师也会从集合的视角进行角的平分线和圆的轨迹教学，并引导学生得出结论：在角内，到角两边距离相等的点的集合是角的平分线；到定点距离等于定长的点的集合是圆。

在几何轨迹教学中进行集合思想的渗透，有利于学生从运动的视角促进基本平面几何图形的理解，从而培养直观想象这一数学核心素养。

教育家布鲁纳说过，掌握数学思想可使数学问题更容易理解和记忆，领会数学思想是通向迁移大道的“光明之路”。在初中数学的教学过程中，考虑到学生的年龄特点、认知规律和教育规律，教师在进行集合思想的挖掘、提炼和渗透时，在教学方法上应充分借助文氏图、数轴、平面直角坐标系等工具，在实践操作过程中注重引导学生体验，在语言上用朴实直观的语言进行描述。

教师具备集合思想方法的知识，了解它们在初中数学教材中的地位，以较高的观点分析和处理初中数学教材，在教学中渗透集合思想，就能帮助学生科学、系统地思考问题，培养学生探索规律、发现真理和解决问题的能力，提升学生的数学核心素养，为高中阶段的数学学习打下坚实基础，实现数学学习的可持续发展。

参考文献

[1] 鲍时主. 集合思想的脉络探析[J]. 试题与研究, 2020（12）

[2] 莫益梅. 生活中的集合思想[J]. 中小学素质教育创新研究大会论文集, 2019（10）

[3] 谷琪. 例谈巧用集合思想解题[J]. 理科爱好者（教育教学）, 2019（06）

[4] ISBN 7-5320-9713-7/G,沪教版《数学》.上海:上海世纪出版集团,上海教育出版社. 2019.12